Пифагоровы штаны и ещё 5 вопросов из геометрии, которые мучили нас со школы
Геометрия – древняя наука, которая помогала ученым и исследователям веками. Сегодня мы расскажем о том, как тень от Солнца дала возможность высчитать диаметр Земли, а так называемые подобные треугольники спасали красноармейцев во время Великой Отечественной войны.

Об удивительных примерах использования геометрических знаний рассказывает Андрей Шелудько, преподаватель математики и основатель онлайн-школы «Точка Знаний».
Например, для создания прямых углов, египтяне использовали обычную веревку с 12 узлами, расположенными на равном расстоянии друг от друга. С помощью этой веревки можно было легко создавать треугольник с соотношением сторон 3:4:5 — он всегда образует прямой угол. Так египтяне использовали геометрические знания задолго до появления формальной математики, чтобы строить свои величественные пирамиды.

Эратосфен заметил, что в день летнего солнцестояния в городе Сиена (нынешний Асуан, Египет) солнце находилось прямо над головой и его лучи падали вертикально, не отбрасывая тени. В то же время в Александрии, расположенной к северу от Сиены, солнечные лучи создавали тень, образуя угол с земной поверхностью.
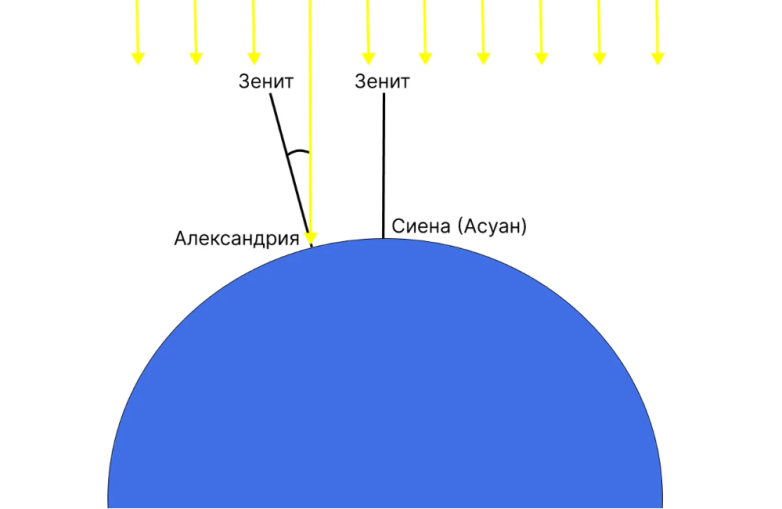
Эратосфен измерил этот угол и обнаружил, что он составляет приблизительно 7,2 градуса. Зная расстояние между Сиеной и Александрией (около 800 километров) и угол падения солнечных лучей в Александрии, Эратосфен предположил, что это расстояние составляет 1/50 окружности Земли. Умножив 800 километров на 50, он получил приблизительное значение окружности Земли — 40 000 км.
Зная это расстояние, он смог вычислить радиус Земли, получив примерное значение — 6200 км. К слову, современные измерения дают для усредненного радиуса Земли величину 6,371 км.
Солдат вытягивал руку с поднятым вверх большим пальцем и прицеливался взглядом на объект таким образом, чтобы частично или полностью заслонить его. Например, длина пальца 7 см, а длина вытянутой руки — 70 см. Если провести воображаемую линию от кончика пальца к плечу, получится прямоугольный треугольник, в котором катеты отличаются в 10 раз.
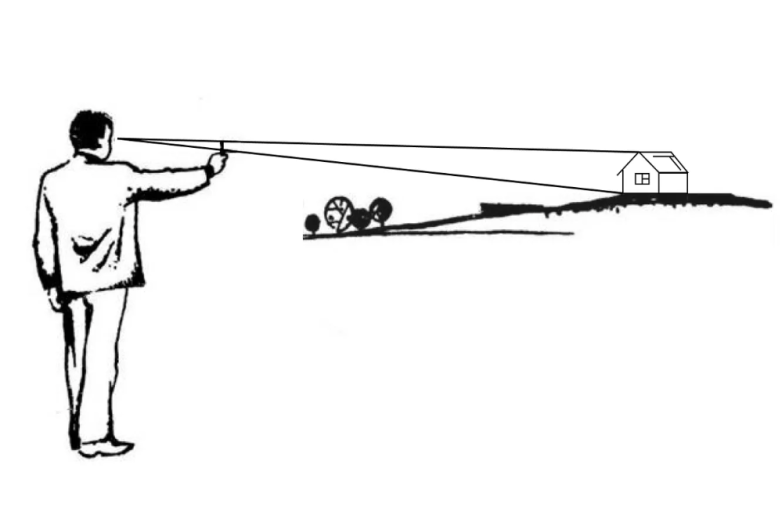
Если объект, например, столб, который солдат заслоняет пальцем, высотой 10 метров, то по правилу подобия треугольников катеты в нем также будут отличаться в 10 раз. Соответственно расстояние от солдата до столба — 100 метров. Таким образом геометрия помогала определять расстояние до противника. Конечно, на войне для определения расстояния в большинстве случаев использовали специальные приборы, но работали они по тому же принципу.
Известен случай, когда советский офицер дал приказ подпилить электрические столбы, стоящие рядом с окопами. Противник обладал ложной информацией о высоте этих столбов, а потому по подсчетам они находились на большем расстоянии. В итоге вражеские снаряды пролетали мимо окопов, не попадая в цель.

Термин «штаны» используется для описания образа, который возникает, когда мы рисуем квадраты на катетах и гипотенузе прямоугольного треугольника. В перевернутом виде эти квадраты напоминают брюки, штанины которых «расползаются» в стороны. Это выражение стало наглядной иллюстрацией для понимания одной из основополагающих теорем геометрии.
К слову о теореме Пифагора, на самом деле ее первым вывел не сам Пифагор – это сделали за 1000 лет до него.
Многие древние строения, включая Парфенон в Афинах, построены с учетом золотого сечения. Греки, хотя и не имели современного понимания математики, интуитивно использовали это соотношение для создания визуально приятных и гармоничных сооружений. Деятели искусства и архитекторы до сих пор, выстраивая композицию в своих работах, придерживаются пропорций, близких к золотому сечению — 3/8 и 5/8.


Об удивительных примерах использования геометрических знаний рассказывает Андрей Шелудько, преподаватель математики и основатель онлайн-школы «Точка Знаний».
Египетская сила
Пирамиды Египта представляют неимоверно сложные с точки зрения архитектуры сооружения. До сих пор ученые из различных областей науки пытаются разгадать тайну такой точности пирамид. Однако некоторые методы, способствующие геометрически правильному возведению сооружений, известны.Например, для создания прямых углов, египтяне использовали обычную веревку с 12 узлами, расположенными на равном расстоянии друг от друга. С помощью этой веревки можно было легко создавать треугольник с соотношением сторон 3:4:5 — он всегда образует прямой угол. Так египтяне использовали геометрические знания задолго до появления формальной математики, чтобы строить свои величественные пирамиды.

Вокруг планеты вместе с Эратосфеном
Другой впечатляющий пример использования геометрии в далекой древности принадлежит греческому ученому Эратосфену Киренскому. В III веке до нашей эры он сумел определить окружность Земли с удивительной для того времени точностью.Эратосфен заметил, что в день летнего солнцестояния в городе Сиена (нынешний Асуан, Египет) солнце находилось прямо над головой и его лучи падали вертикально, не отбрасывая тени. В то же время в Александрии, расположенной к северу от Сиены, солнечные лучи создавали тень, образуя угол с земной поверхностью.

Эратосфен измерил этот угол и обнаружил, что он составляет приблизительно 7,2 градуса. Зная расстояние между Сиеной и Александрией (около 800 километров) и угол падения солнечных лучей в Александрии, Эратосфен предположил, что это расстояние составляет 1/50 окружности Земли. Умножив 800 километров на 50, он получил приблизительное значение окружности Земли — 40 000 км.
Зная это расстояние, он смог вычислить радиус Земли, получив примерное значение — 6200 км. К слову, современные измерения дают для усредненного радиуса Земли величину 6,371 км.
На расстоянии вытянутой руки
Во времена Великой Отечественной войны один урок из геометрии спасал солдатам жизни — они использовали подобные треугольники для определения расстояний до объекта на поле боя.Солдат вытягивал руку с поднятым вверх большим пальцем и прицеливался взглядом на объект таким образом, чтобы частично или полностью заслонить его. Например, длина пальца 7 см, а длина вытянутой руки — 70 см. Если провести воображаемую линию от кончика пальца к плечу, получится прямоугольный треугольник, в котором катеты отличаются в 10 раз.

Если объект, например, столб, который солдат заслоняет пальцем, высотой 10 метров, то по правилу подобия треугольников катеты в нем также будут отличаться в 10 раз. Соответственно расстояние от солдата до столба — 100 метров. Таким образом геометрия помогала определять расстояние до противника. Конечно, на войне для определения расстояния в большинстве случаев использовали специальные приборы, но работали они по тому же принципу.
Известен случай, когда советский офицер дал приказ подпилить электрические столбы, стоящие рядом с окопами. Противник обладал ложной информацией о высоте этих столбов, а потому по подсчетам они находились на большем расстоянии. В итоге вражеские снаряды пролетали мимо окопов, не попадая в цель.
Пифагоровы штаны
Выражение «Пифагоровы штаны» связано с известной теоремой Пифагора, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Это выражение часто звучит в виде стихотворной строки: «Пифагоровы штаны во все стороны равны».
Термин «штаны» используется для описания образа, который возникает, когда мы рисуем квадраты на катетах и гипотенузе прямоугольного треугольника. В перевернутом виде эти квадраты напоминают брюки, штанины которых «расползаются» в стороны. Это выражение стало наглядной иллюстрацией для понимания одной из основополагающих теорем геометрии.
К слову о теореме Пифагора, на самом деле ее первым вывел не сам Пифагор – это сделали за 1000 лет до него.
Золотое сечение в архитектуре
Золотое сечение, также известное как «золотое отношение» или «божественная пропорция», обозначается греческой буквой φ (фи). Это отношение составляет приблизительно 1.618. Еще в Древней Греции математики, такие как Пифагор и Евклид, исследовали геометрические свойства золотого сечения. Они описывали это отношение как разделение отрезка на две части таким образом, что отношение всей длины к большей части равно отношению большей части к меньшей.Многие древние строения, включая Парфенон в Афинах, построены с учетом золотого сечения. Греки, хотя и не имели современного понимания математики, интуитивно использовали это соотношение для создания визуально приятных и гармоничных сооружений. Деятели искусства и архитекторы до сих пор, выстраивая композицию в своих работах, придерживаются пропорций, близких к золотому сечению — 3/8 и 5/8.

Только зарегистрированные и авторизованные пользователи могут оставлять комментарии.