Как великого Эйнштейна разыграли простой задачкой

Как думаете, мог ли великий Альберт Эйнштейн оставить нерешенной хоть одну задачу? Правильно — не мог. Тем не менее существует одна вроде бы простая логическая загадка, которая заставила великого ученого хорошенько поскрипеть мозгами. И если вы уверены, что в руках у вас верное решение, — не спешите. Подумайте, почитайте условие, посчитайте еще раз. А уже потом можете смело претендовать на звание того, кто оказался умнее Эйнштейна.

На дворе 1934 год. Один из основателей гештальтпсихологии Макс Вертгеймер, автор одного из знаменитых высказываний, что целое есть нечто большее, чем сумма его частей, со скуки пишет письмо своему хорошему приятелю. Приятель этот не простой, а тот самый великий ученый Альберт Эйнштейн, который к тому моменту уже разработал несколько значительных физических теорий, дюжину раз был номинантом на Нобелевскую премию и таки получил ее в ноябре 1922 года. Разумеется, письмо Эйнштейну было с подвохом, то бишь с задачей, как любил великий физик.
Итак, вот ее условие. Есть старый автомобиль, которому надо сначала въехать на холм, а затем с него спуститься. Расстояние до вершины холма ровно одна миля, такой же длины и спуск. Общий путь соответственно две мили. Средняя скорость при подъеме автомобиля на холм — 15 миль/час.

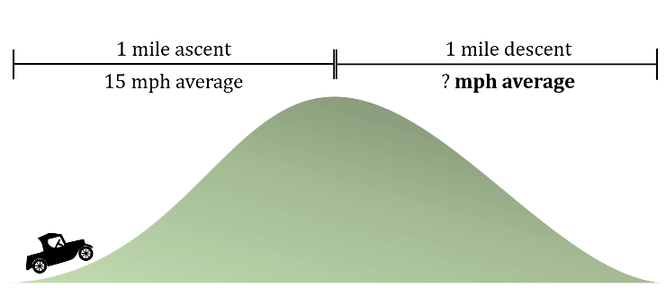
Внимание, вопрос: с какой скоростью должен ехать автомобиль с холма, чтобы средняя скорость движения на всем пути составила ровно 30 миль/час?
Давайте запишем условие для наглядности:
Vср = 30 миль/час
Vвверх = 15 миль/час
Vвниз =?
Хватаемся за карандаш, и поехали. Судя по многочисленным спорам в соцсетях и попыткам решить эту почти столетнюю задачу, многие из вас сразу же составят уравнение и найдут решение в два действия:
Vср = Vвверх + Vвниз / 2
Отсюда:
Vвниз = 2 * Vср — Vвверх = 2 * 30 — 15 = 45 миль/час
Ура, вы сделали это! Только не спешите праздновать — решение неправильное, и мы сейчас объясним почему. Есть вроде бы два похожих, но на деле совершенно разных значения: среднее арифметическое и средняя скорость. Формулой в начале вашего решения вычисляется первое значение, но оно нам вообще ни к чему. В тоже время второе значение равно отношению пройденного пути ко времени движения. Не переживайте, со второго раза все точно получится. Для начала давайте вычислим время преодоления всего пути, равного двум милям:
30 миль/час = 2 мили / Tобщее
Отсюда:
Tобщее = 2 мили / 30 миль/час = 1 / 15 часа = 4 минуты
Теперь нам надо вычислить время, за которое машина въедет на холм:
Tвверх = 1 миля / 15 миль/час = 1 /15 часа = 4 минуты
Улавливаете? Окей, давайте по буквам. У нас получилось, что время на подъем равно 4 минутам, а общее время равно… Погодите, тоже 4 минуты! Теперь понимаете? Времени на спуск попросту нет, машина одновременно должна быть на вершине холма и в конце пути, что в принципе невозможно. Проказник Вертгеймер придумал для Эйнштейна задачу без правильного ответа чем здорово поднял настроение другу. И продолжает поднимать всем остальным вот уже без малого сто лет!