Простейшая задача из ЕГЭ — решите ли её вы?
Мы частенько любим ругать школьные задачки, дескать, условия в них иногда бывают настолько абсурдными и несуразными, что напрочь сбивает с толку. И вместо того, чтоб после прочтения условия приступить к решению, мы тратим время на критику. Но вот «бородатая» задачка из базовой математики, в которой с условием все в порядке. Даже у старшеклассников-гуманитариев на ее решение уходят считаные минуты, а сколько времени понадобится вам?

Итак, вот условие.
В пункте обмена можно совершить одну из двух операций:
2 золотые монеты обменять на 3 серебряные и 1 медную
5 серебряных монет обменять на 3 золотые и 1 медную
У Александра в кармане только серебряные монеты. Он несколько раз сходил в обменник, после чего серебряных монет у него стало меньше, появилось 100 медных, а золотых не появилось вовсе. На сколько уменьшилось количество серебряных монет у Александра в кармане?
Имейте в виду, что задача не содержит никаких логических ловушек, вам понадобиться только внимательность, базовые знания математики и немного смекалки. Все просто! Прежде чем читать решение ниже, попробуйте победить задачку сами. Все остальные — переходим к следующей главе.
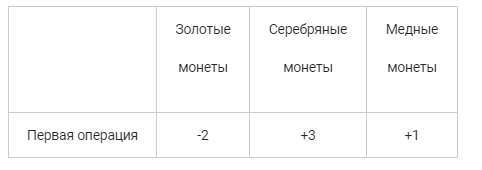
Операция второго типа — у Александра становится на 5 серебряных монет меньше, зато золота и серебра больше на 3 и 1 монеты соответственно:
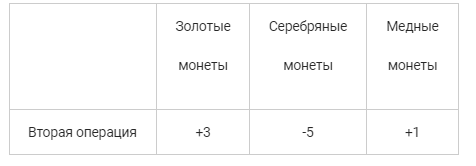
Мы не знаем, сколько операций первого и второго типа было произведено, так что их количество запишем как х и у:
Зная из условия, что в результате всех манипуляций с монетами у Александра прибавилось 100 медных монет, а количество золотых не изменилось. Запишем два уравнения в систему:
1х + 1у = 100 (медные монеты)
-2х + 3у = 0 (золотые монеты)
Для начала выразим из первого уравнения х, затем подставим решение в уравнение с у:
х = 100 — у
-2 (100 — у) + 3у = 0
-200 + 5у = 0
у = 40
х = 100 — 40 = 60
Итак, мы нашли количество операций первого и второго типов: 60 и 40 соответственно. Теперь финишная прямая: выясняем, на сколько изменилось количество серебряных монет у Александра.
3х — 5у = 3 * 60 — 5 * 40 = 180 -200 = — 20
Вот и ответ — количество серебряных монет сократилось на 20. Мы же предупреждали, всё очень просто.

Итак, вот условие.
В пункте обмена можно совершить одну из двух операций:
2 золотые монеты обменять на 3 серебряные и 1 медную
5 серебряных монет обменять на 3 золотые и 1 медную
У Александра в кармане только серебряные монеты. Он несколько раз сходил в обменник, после чего серебряных монет у него стало меньше, появилось 100 медных, а золотых не появилось вовсе. На сколько уменьшилось количество серебряных монет у Александра в кармане?
Имейте в виду, что задача не содержит никаких логических ловушек, вам понадобиться только внимательность, базовые знания математики и немного смекалки. Все просто! Прежде чем читать решение ниже, попробуйте победить задачку сами. Все остальные — переходим к следующей главе.
Решение
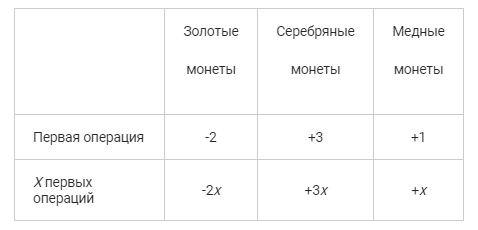
Давайте для начала представим себя бухгалтерами и распишем каждую обменную операцию. Операция первого типа — две золотых монеты Александр отдает и получает 3 серебром и 1 медью:
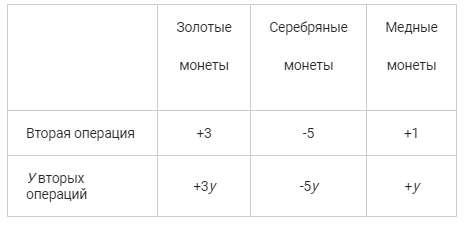
Операция второго типа — у Александра становится на 5 серебряных монет меньше, зато золота и серебра больше на 3 и 1 монеты соответственно:

Мы не знаем, сколько операций первого и второго типа было произведено, так что их количество запишем как х и у:


Зная из условия, что в результате всех манипуляций с монетами у Александра прибавилось 100 медных монет, а количество золотых не изменилось. Запишем два уравнения в систему:
1х + 1у = 100 (медные монеты)
-2х + 3у = 0 (золотые монеты)
Для начала выразим из первого уравнения х, затем подставим решение в уравнение с у:
х = 100 — у
-2 (100 — у) + 3у = 0
-200 + 5у = 0
у = 40
х = 100 — 40 = 60
Итак, мы нашли количество операций первого и второго типов: 60 и 40 соответственно. Теперь финишная прямая: выясняем, на сколько изменилось количество серебряных монет у Александра.
3х — 5у = 3 * 60 — 5 * 40 = 180 -200 = — 20
Вот и ответ — количество серебряных монет сократилось на 20. Мы же предупреждали, всё очень просто.
Только зарегистрированные и авторизованные пользователи могут оставлять комментарии.
+2
Эк как «завернул», а ведь всё гораздо проще. Ну да ладно…
- ↓
+3
"… Теперь по арифметике… Берите доску. Какая следующая задача?
Петя плюет на доску и стирает рукавом. Учитель берет задачник и диктует:
— «Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?» Повторите задачу.
Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.
— Для чего же это вы делите? Постойте! Впрочем, так… продолжайте. Остаток получается? Здесь не может быть остатка. Дайте-ка я разделю!
Зиберов делит, получает 3 с остатком и быстро стирает.
«Странно… — думает он, ерoша волосы и краснея. — Как же она решается? Гм!.. Это задача на неопределенные уравнения, а вовсе не арифметическая»…
Учитель глядит в ответы и видит 75 и 63.
«Гм!.. странно… Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то».
— Решайте же! — говорит он Пете.
— Ну, чего думаешь? Задача-то ведь пустяковая! — говорит Удодов Пете. — Экий ты дурak, братец! Решите уж вы ему, Егор Алексеич.
Егор Алексеич берет в руки грифель и начинает решать. Он заикается, краснеет, бледнеет.
— Эта задача, собственно говоря, алгебраическая, — говорит он. — Ее с иксом и игреком решить можно. Впрочем, можно и так решить. Я, вот, разделил… понимаете? Теперь, вот, надо вычесть… понимаете? Или, вот что… Решите мне эту задачу сами к завтраму… Подумайте…
Петя ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из угла в угол.
— И без алгебры решить можно, — говорит Удодов, протягивая руку к счетам и вздыхая. — Вот, извольте видеть…
Он щелкает на счетах, и у него получается 75 и 63, что и нужно было.
— Вот-с… по-нашему, по-неученому."
А. П. Чехов, «Репетитор»
Всё уже придумано до нас…
Пы.Сы. Решение этой задачки на счётах, без иксов и игреков, подробно расписано много где, да хотя бы — в «Занимательной математике» Перельмана.
- ↓
+10
Предложенное решение хорошо иллюстрирует деградацию российского образования. Задачка действительно элементарная и решается в три шага:
Дано: 5 серебряных = 3 золотых + 1 медная и 2 золотых = 3 серебряных + 1 медная
Умножаем первое уравнение на 2, а второе на 3, получаем:
10с=6з+2м и 6з=9с+3м подставляем второе уравнение в первое и получаем:
10с=9с+5м, т.е. 1с=5м
Соответственно на получение 100 медных монет было истрачено 100/5=20 серебряных монет
Как видите все элементарно просто на уровне 5 класса средней школы!
- ↓
+5
Да, это решение изящнее и проще. Но ведь нужно было догадаться уравнять количество золотых монет в обоих выражениях. А логические размышления в болонской системе обучения совершенно не приветствуются, как и установление причинно-следственных связей в различных процессах.
- ↑
- ↓
-1
Класс!
- ↓