5 самых трудных головоломок в мире, после которых мозг будет просить вас о пощаде
Человек использовал ум, чтобы достичь небывалых высот в науке и технике, но порой игры разума носили не только сугубо практический и утилитарный характер: так на свет появилось множество различных головоломок, для решения которых приходится основательно «пораскинуть мозгами». Пять из них вы найдёте в этой подборке.
Одной из самых популярных в мире разновидностей кроссворда является судоку — японская головоломка с числами. Её принцип несложен, поэтому многие любители стараются создать свои варианты. В 2012-м году финский математик Арто Инкала заявил, что разработал «самую трудную в мире судоку».
Как сообщает британская газета «The Telegraph», если самые простые из распространённых вариантов судоку по шкале сложности обозначить, как «1», а наиболее сложные из популярных оценить на «5», то предложенный математиком вариант тянет на «11».
Эта логическая задача за авторством американского философа и логика Джорджа Булоса была впервые опубликована в итальянской газете «la Repubblica» в 1992-м году. В комментариях к загадке Булос делает важное замечание: каждому богу можно задать более одного вопроса, но больше трёх задавать нельзя.
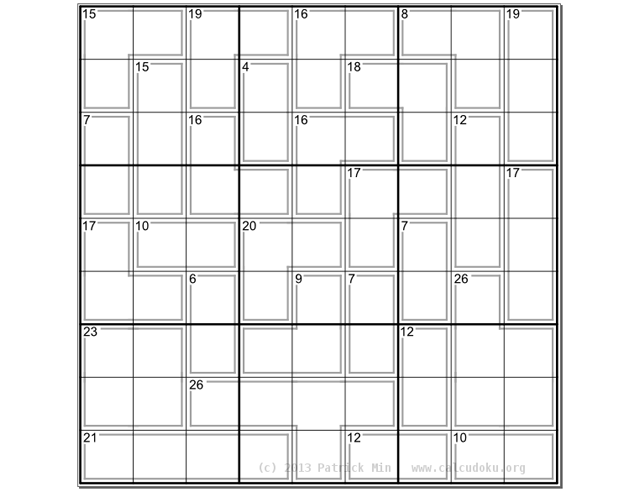
Одной из популярных разновидностей судоку является сум-до-ку, её ещё называют «убийца судоку». Вся разница в том, что в сум-до-ку заданы дополнительные числа — суммы значений в группах клеток, при этом числа, содержащиеся в группе, не должны повторяться. В популярном сервисе головоломок Calcudoku.org можно отследить рейтинг сложности опубликованных задач, одной из них стала сум-до-ку, которая изображена здесь.
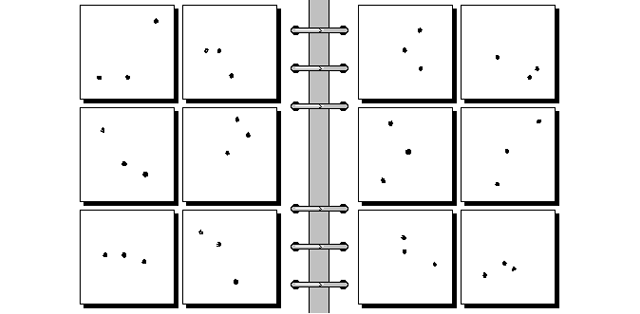
Этот тип головоломки изобрёл выдающийся русский кибернетик, основоположник теории распознавания образов Михаил Моисеевич Бонгард: в 1967-м году он впервые опубликовал одну из них в своей книге «Проблема узнавания». Широкую популярность «проблемы Бонгарда» обрели, когда знаменитый американский физик и информатик Дуглас Хофштадтер упомянул о них в своём труде «Гёдель, Эшер, Бах: эта бесконечная гирлянда».
Два самых сложных примера таких задач взяты с Foundalis.com, для их решения вы должны найти правило, которому соответствуют шесть изображений на левой странице, но под которое не подходят шесть картинок в правой части.
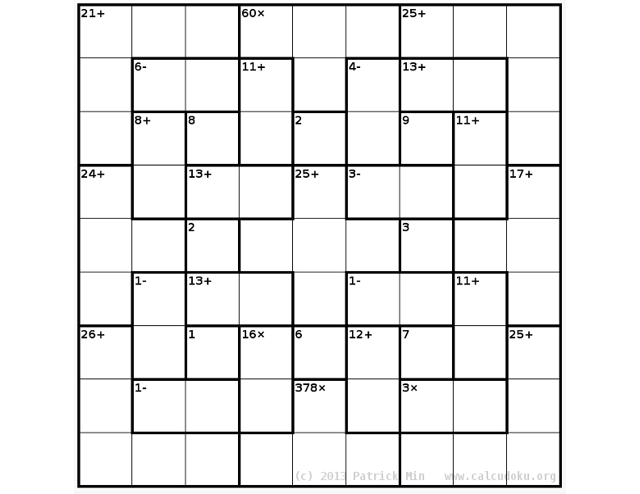
Этот вид судоку похож на сум-до-ку, но, во-первых, для вычисления значения клеток используются любые арифметические операции, а не только сложение, во-вторых, поле может быть квадратом любого размера (количество клеток не ограничено), и в-третьих, в отличие от судоку, здесь необязательно должны присутствовать подсказки от 1-го до 9-ти в каждом квадрате 3х3. Такие задачи разработал японский учитель математики Тетсуя Миямото.
Здесь вы можете попробовать разобраться с самой трудной кальку-доку. Лишь 9,6% постоянных посетителей ресурса, где она была опубликована, удалось её решить.
1. Самая трудная в мире судоку

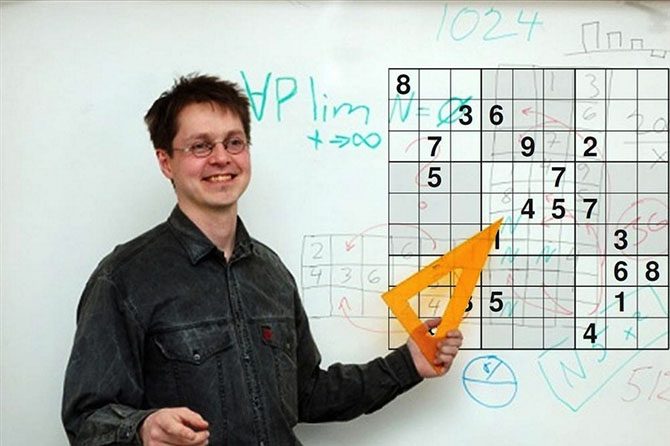
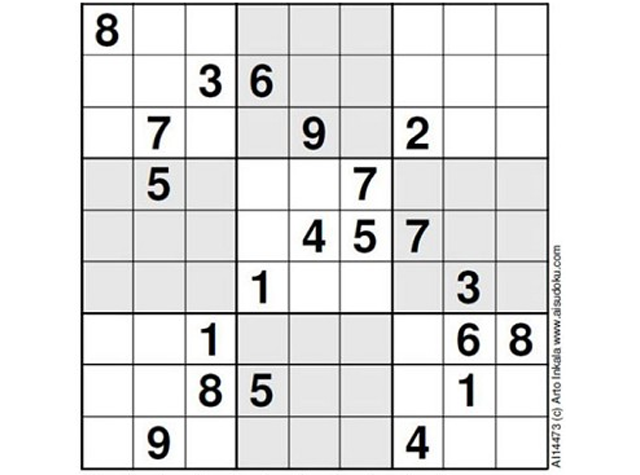
Одной из самых популярных в мире разновидностей кроссворда является судоку — японская головоломка с числами. Её принцип несложен, поэтому многие любители стараются создать свои варианты. В 2012-м году финский математик Арто Инкала заявил, что разработал «самую трудную в мире судоку».

Как сообщает британская газета «The Telegraph», если самые простые из распространённых вариантов судоку по шкале сложности обозначить, как «1», а наиболее сложные из популярных оценить на «5», то предложенный математиком вариант тянет на «11».
2. Самая сложная логическая головоломка
Есть три бога, A, B, и C, один из которых бог истины, другой бог лжи и третий бог случая, причём неясно, кто из них кто. Бог истины всегда говорит правду, бог лжи обманывает, а бог случая может сказать и то, и другое в произвольном порядке. Необходимо определить, кем является каждый из богов, задав три вопроса, на которые можно ответить «да» или «нет», при этом каждый вопрос задаётся только одному богу. Боги понимают вопросы, но отвечают на своём языке, в котором есть слова «da» и «ja», но неизвестно, какое слово обозначает «да», а какое «нет».Эта логическая задача за авторством американского философа и логика Джорджа Булоса была впервые опубликована в итальянской газете «la Repubblica» в 1992-м году. В комментариях к загадке Булос делает важное замечание: каждому богу можно задать более одного вопроса, но больше трёх задавать нельзя.
3. Самая трудная в мире сум-до-ку

Одной из популярных разновидностей судоку является сум-до-ку, её ещё называют «убийца судоку». Вся разница в том, что в сум-до-ку заданы дополнительные числа — суммы значений в группах клеток, при этом числа, содержащиеся в группе, не должны повторяться. В популярном сервисе головоломок Calcudoku.org можно отследить рейтинг сложности опубликованных задач, одной из них стала сум-до-ку, которая изображена здесь.
4. Самая сложная «Проблема узнавания» Бонгарда

Этот тип головоломки изобрёл выдающийся русский кибернетик, основоположник теории распознавания образов Михаил Моисеевич Бонгард: в 1967-м году он впервые опубликовал одну из них в своей книге «Проблема узнавания». Широкую популярность «проблемы Бонгарда» обрели, когда знаменитый американский физик и информатик Дуглас Хофштадтер упомянул о них в своём труде «Гёдель, Эшер, Бах: эта бесконечная гирлянда».
Два самых сложных примера таких задач взяты с Foundalis.com, для их решения вы должны найти правило, которому соответствуют шесть изображений на левой странице, но под которое не подходят шесть картинок в правой части.
5. Наиболее трудная головоломка кальку-доку

Этот вид судоку похож на сум-до-ку, но, во-первых, для вычисления значения клеток используются любые арифметические операции, а не только сложение, во-вторых, поле может быть квадратом любого размера (количество клеток не ограничено), и в-третьих, в отличие от судоку, здесь необязательно должны присутствовать подсказки от 1-го до 9-ти в каждом квадрате 3х3. Такие задачи разработал японский учитель математики Тетсуя Миямото.
Здесь вы можете попробовать разобраться с самой трудной кальку-доку. Лишь 9,6% постоянных посетителей ресурса, где она была опубликована, удалось её решить.
Только зарегистрированные и авторизованные пользователи могут оставлять комментарии.
0
Спасибо за головоломки.
- ↓
+1
Во второй задаче для того, чтобы понять язык, надо спросить А — «А всегда говорит правду?», Б — «Б всегда говорит правду?» ну и С соответственно. (Вопросы однотипные, но все-таки разные, кажется, это допускается условиями задачи). Большинство ответов будут означать слово «Да». Дальше спрашиваем у каждого из них «1+1=2», «2+2=4», «3+3=6» и точно выявляем либо лжеца либо правдивого, в зависимости от того, как ответит неопределенный. А потом у выявленного можно точно узнать, кто из оставшихся бог неопределенности. Довольно несложно, или я в условиях задачи чего то недопоняла?
- ↓
0
Не пойдет… Всего вопросов должно быть не более трех. То есть одному богу можно задать более одного вопроса, но всего в совокупности — не более трех вопросов. А иначе действительно все просто…
- ↑
- ↓
0
А-а. Хм-м-м. Тогда придется подумать, как слепить все вопросы в один. Что-то типа «если 1+1=2, то скажи мне, всегда ли ты говоришь правду...» В общем, надо подумать.
- ↑
- ↓
0
Ну, наверное поэтому и утверждается, что она самая сложная… Мне тоже пока ничего толкового в голову не приходит… Ясно только, что вопросы должны по максимуму включать информацию обо всех трех богах. Чем-то это напоминает старую задачку: типа, в неком государстве вас приговорили к смерти. Но дали шанс — привели в комнату, в которой 2 двери. Одна ведет на свободу, другая — в пропасть (ну или за другой палач, неважно...). Неизвестно, какая из них куда ведет. У каждой двери сидит стражник. Известно, что один из стражников — лгун (врет на любой вопрос), а второй — правдив. Тоже неизвестно, кто из них кто… Разрешено задать любому из них только один вопрос, на который он должен ответить «да» или «нет». После этого надо выбрать дверь на свободу…
Вот тут тоже вопрос должен объединять в себе информацию и о стражниках, и о двери.
И в этой задаче что-то похожее… Чую я, в первую очередь надо как-то идентифицировать бога случая, он самый опасный.
- ↑
- ↓
0
Вот подойдет ли тут условие «если»? Оно прибавляет к вариантам ответа «да» и «нет» еще и отсутствие ответа, поэтому наверное это будет нарушать условие задачи. А так, если спросить «если ты согласен, что 1+1=2, то ответь, DA это „да“? — это позволит отделить какого-нибудь определенного бога от бога неопределенности. Хотя… ладно, буду думать дальше :)
- ↑
- ↓
0
ну если богов действительно зовут а в с-то пойдёт-а вообще с примерами здорово придумали
- ↑
- ↓
+1
На какую хрень люди время тратят!!!
- ↓